April is Mathematics and Statistics Awareness month! Charlotte Cook, senior risk analyst, and Flavie Vial, statistician, share with us one of the many ways mathematics is used within APHA to inform decision-making.
There are many things to rejoice come April time, including the spring bird migration, the blooming of woodland wild flowers and hot cross buns. Since 1986, this month also marks a time to increase the visibility of mathematics as a field of study and to communicate the power and intrigue in mathematics to a larger audience.
Originating as Mathematics Awareness Week in the United States, Mathematics Awareness Month is now an international event held to remind everyone of the importance of this branch of science to our daily lives - from internet security, to sport, disease and climate change.
Mathematics and statistics are important drivers of innovation in our increasingly complex technological world.
In APHA, mathematics is used to inform day-to-day decisions, provide evidence TO support policy development and support operational staff in emergencies. The techniques used cover geographical information systems (GIS), risk and epidemiological analysis, mathematical and statistical modelling, and many more.
Here’s just one of the ways mathematics is used within our teams to inform decision-making.
QUADS EpiTeam

The QUADS EpiTeam is an international group of epidemiological mathematical modellers. It was founded in 2005, specifically to look at how mathematical modelling is involved in decision making.
The name comes from the 4 core countries that make up the group; New Zealand, Australia, Canada and the United States. Other countries that have joined the group for a time include Ireland, the Netherlands, Sweden and the UK.
Initially, the EpiTeam used foot and mouth disease (FMD) as a case study because all the countries involved have the same international status with regards to FMD, i.e. they are recognised as FMD free countries where vaccination is not practised. To retain such high health status, each country has contingency policy and plans in place on how to deal with an outbreak.
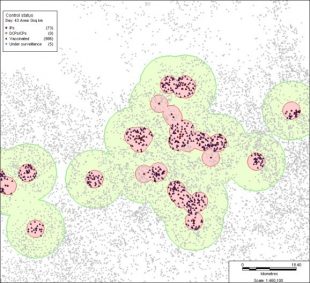
Where a disease like FMD is not present in a country, it can be very difficult to predict the effects that changes in policies, and contingency plans, may have on the control of the disease. In these cases, a mathematical model can be a very useful tool.
The mathematical model describes the biological system involved (whether livestock or wildlife), how disease may spread naturally, and also what may happen when you introduce an action that is designed to slow down disease spread. The
UK has a mathematical model, named Exodis, which describes how FMD might spread through the UK livestock industry.
Using the model we can test different interventions to stop or slow the spread of disease (e.g. setting up vaccination zones and/or zones under increased surveillance around infected farms) and immediately see how effective they may be.
As we haven’t had many outbreaks of FMD in the UK, it’s very hard to say how accurate our model is. Normally, we would simulate outbreaks in a model and then compare them to real outbreaks and see how similar they are.
So the EpiTeam developed a method that was designed to look at several mathematical models for FMD and compare how they performed against each other - this is called ‘comparative model validation’. Since each country has independently produced a mathematical model, they are all slightly different but designed to achieve the same thing.
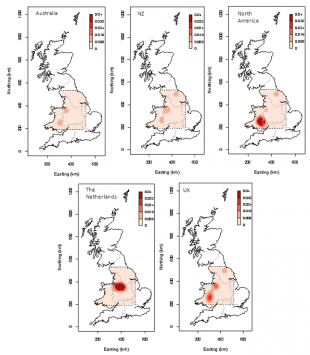
To compare the models against each other, the EpiTeam came up with a ‘shared challenge problem’ - the beginning of a hypothetical FMD outbreak.
The different models were all prepared with an identical set of data of the UK livestock industry and the hypothetical FMD outbreak. The models then simulated a number of different FMD interventions and we measured how big each simulated outbreak became.
The team then looked at all the outputs of the models and how similar the predictions were on the length of the outbreak and how many farms were infected.
Although the models might not have agreed on the exact length of time each outbreak lasted, they did agree that using some interventions (e.g. depopulating all infected farms and vaccinating at-risk animals within a given radius) shortened the length of an outbreak.
These results help us build confidence in our models, and although they were built independently, they generally agree on the overall effectiveness of interventions to help stop or slow the spread of FMD. A complete journal article on the project can be found in the following paper:
Roche, S.E., et al., Evaluating vaccination strategies to control foot-and-mouth disease: a model comparison study. Epidemiology and Infection, 2015. 143(6): p. 1256-75
In summary
While mathematics and statistics are important and fascinating branches of science in themselves, there are many other benefits to their study. Both disciplines are about pattern and structure. They are about finding patterns, in widely different areas of science and technology, and using them to:
- explain our ideas with clarity, coherence and precision
- predict and control natural happenings.
When we think of mathematics, we often visualise long numeric equations, seas of symbols or long spreadsheets stacked with graphics. What we don’t realise though is that these complex equations are in fact roads to simplicity, allowing us all to devise better, faster, and smarter solutions to the dozens of problems we are, often subconsciously, faced with every day.
Follow APHA on Twitter and don't forget to sign up to email alerts.

1 comment
Comment by Mark Chambers posted on
Fascinating and well written article. Thank you.